Himmelskoordinaten

Die Erde ist fast kugelförmig. Wenn sie auch nicht genau der Form einer Kugel entspricht (Rotationsellipsoid), kann man sie trotzdem in ein Koordinatensystem einbinden, das einer Kugel entspricht.

Ein Koordinatensystem ist die Voraussetzung für die Darstellung von Messwerten. Zwei Veränderliche wie z.B. x und y stellt man in der Mathematik durch 2 senkrecht aufeinander sich kreuzende Achsen dar (der x-Achse auch Abszisse genannt und im rechten Winkel dazu, die y-Achse auch Ordinate genannt). Der Kreuzungspunkt beider Achsen ist der „Nullpunkt“ bzw. fester Referenzpunkt, der auch „Ursprung“ genannt wird. Jeden Punkt in einer ebene Fläche kann man auf diese Weise einfach beschreiben, indem man z.B. für die Länge die x- Achse und für die Breite die y- Achse als Massstab nimmt.

Da wir auf der Oberfläche der Erde leben, haben wir es auch mit einer Fläche zu tun, wenn wir diese Oberfläche beschreiben wollen.

(Allerdings ändert sich die Geometrie einer Kugelfläche (sphärische Trigonometrie) gegenüber einer ebenen Fläche (ebene Trigonometrie). Wir können also jeden Punkt der Erdoberfläche durch zwei Dimensionen oder Koordinaten darstellen, da wir es ja hier, wie gesagt, mit einer Fläche zu tun haben.)

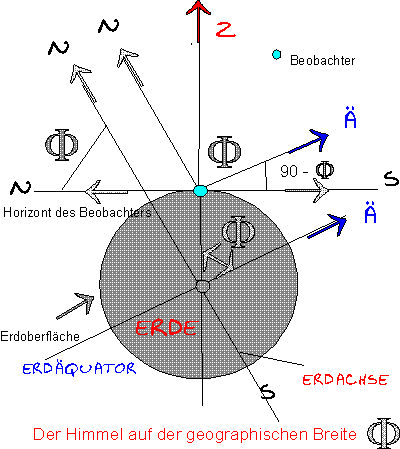
Wenn wir bei der Analogie der x- und y- Achse bleiben, so können wir für die x-Achse die geographische Länge der Erde nehmen, die den Umfang des Äquators in 360° einteilt. Als Referenzpunkt wurde in einer internationalen Vereinbarung der Längengrad gewählt, der durch Greenwich bei London (der sogenannte Null-Meridian) geht. Nach Westen wird positiv (+) gezählt, nach Osten negativ (-). Unsere Sternwarte liegt z.B. auf 9° Ost oder einfach -9° Länge. Für die y- Achse, um im Bild zu bleiben, wird die geographische Breite angegeben. Hier ist der Nullpunkt oder besser die Null-Linie der Äquator. Nach Norden, also nördlich des Äquators wird positiv (+) gezählt, nach Süden negativ (-). Der Nordpol liegt also bei +90°, und der Südpol bei -90° Breite. Der nördliche Wendekreis liegt bei +23,5° und der südliche bei -23,5° Breite usw.

Mit diesem System können wir jeden Punkt der Erde präzise beschreiben. Dies ist auch die Basis für die Beschreibung der Positionen von Himmelsobjekten am Sternenhimmel.

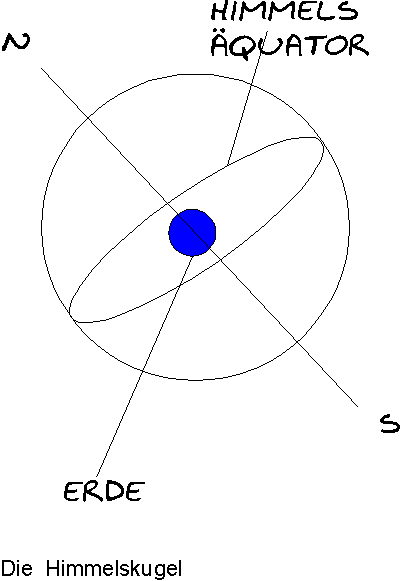
Mit dem Koordinatensystem für Himmelsobjekte übernimmt man im Prinzip die antiken Vorstellungen der Himmelssphäre die sich um die feststehende Erde dreht. Obwohl das Gegenteil richtig ist, eignet sich dieses System hervorragend die Positionen am Himmel zu beschreiben. Hier musste ein Nullpunkt festgelegt werden, der sich mit der Himmelssphäre dreht, so dass man von diesem Punkt aus die feststehenden Koordinaten in Atlanten und Sternkalendern festhalten kann und dass man einen Bezugspunkt für die veränderlichen Positionen von Planeten, Sonne, Mond, Kometen usw. hat.

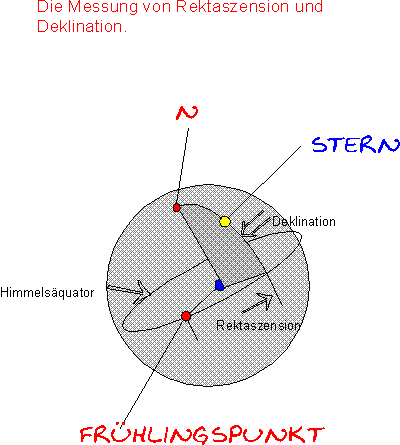
Dieser Punkt ändert seine Position entsprechend 360° in ca. 26 000 Jahren. Daher wird zu der Rektaszension und Deklination das Äquinoktium mit einer Jahreszahl angegeben, das ist der Zeitpunkt für den die Daten gelten. Dieser Nullpunkt ist der sogenannte Frühlingspunkt, also einer der Schnittpunkte von Ekliptik und Äquator. Die Bezugslinie für die Deklination (D) ist der Himmelsäquator, der genau über dem Erdäquator liegt. Befindet man sich auf dem Erdäquator, so steht der Himmelsäquator genau im Zenit. Dasselbe gilt natürlich für die anderen Punkte wie etwa Nordpol oder Südpol.

Als Ekliptik bezeichnet man die scheinbare Bahn der Sonne um die Erde. Sie ist zum Äquator um 23,5° geneigt und erzeugt somit zwei Schnittpunkte. Als Frühlingspunkt bezeichnet man ihn deshalb weil die Sonne in ihrer aufsteigenden Bahn im Frühlingsanfang durch diesen Punkt wandert. Auf der absteigenden Bahn kreuzt die Sonne den Äquator im Herbstpunkt.

Das was wir auf der Erde als Längengrad bezeichnen und auf den Null-Meridian beziehen, das nennt man jetzt „Rektaszension“ bezogen auf den Frühlingspunkt als Nullpunkt und nach Osten gezählt, und zwar nur nach Osten, es gibt keine negative Rektaszension. Die Werte werden in „Stunden, Minuten und Sekunden“ angegeben.

Den Abstand zum Äquator nennt man „Deklination„. Sie entspricht, wie auf der Erde auch, dem Winkelabstand zum Äquator in „Grad, Bogenminuten, und Bogensekunden“ nördlich mit + und südlich des Äqators mit – Vorzeichen.

Die Umrechnung der Zeit von Stunden, Minuten und Sekunden in Bogenmaße, entsprechend der Teilung von 360° in 24 Stunden, ergibt:

Rektaszension	Winkel
1 Stunde	15°
1 Minute	15′ (Bogenminuten) = 1/4°
1 Sekunde	15″ (Bogensekunden) = 1/240°

Mit den beiden Größen Rektaszension und Deklination können wir somit jeden Punkt am Himmel so genau beschreiben wie es unsere technische Ausrüstung am Teleskop zulässt.

Als nächsten Schritt müssen wir dieses Himmelskoordinatensystem mit unserer Erde koordinieren. Da alle Himmelsobjekte sich im Bezug zur Erde bewegen, man denke nur an die Sonne oder den Mond oder auch an Sterne und Sternbilder, wie sie im Osten aufgehen und im Westen untergehen, kommt jetzt die Zeit ins Spiel, da sich die Himmelssphäre scheinbar um die Erde dreht, und damit die Objekte je nach Zeitpunkt an einer anderen Stelle am Himmel stehen.

Hier muss man wieder einen neuen Begriff einführen und zwar die „Sternzeit„.

Aber zuerst noch zum „Stundenwinkel“ eines Objektes. Er hängt nur von der Rektaszension eines Objektes ab und entspricht der Zeit, die das Himmelsobjekt braucht, um vom Süd-Meridian an seine aktuelle Position zu gelangen.

Die Sternzeit ist nun einfach der Stundenwinkel des Frühlingspunktes. Wenn der Frühlingspunkt durch den Meridian läuft, ist es 0h Sternzeit. Drei Stunden nach Meridiandurchgang des Frühlingspunktes ist es 3h Sternzeit.

Diese Zeit weicht von unserer üblichen Tageszeit, der Sonnenzeit, ab. Der mittlere Sonnentag ist 24 Std. lang. Er gibt an, wie lange die Sonne im Mittel braucht, um einmal scheinbar um die Erde zu wandern, also von Meridian zu Meridian. Da sich die Sonne scheinbar einmal mehr in einem Jahr um die Erde dreht als die Sterne – das liegt daran, dass sich die Erde in einem Jahr um die Sonne dreht, die Sterne jedoch immer in ihrer Position bleiben – ist die Sternzeit pro Tag um den Betrag geringer als die mittlere Sonnenzeit, der 24 Stunden / 365,25 Tagen im Jahr entspricht.

Ein Sternentag dauert also nur 23h56m04s. Man kann also täglich eine Abweichung der Sternzeit von der Sonnenzeit von 3 min 56 sek. feststellen, der Effekt ist kummulativ, das heißt die Differenz zwischen Stern- und Sonnenzeit wird immer größer, bis sie nach einem Jahr am Frühlingsanfang wieder zusammentreffen.

Die Sternzeit zählt man vom Südmeridian eines Beobachtungsortes nach Westen wieder in Stunden, Minuten und Sekunden. Da der Südmeridian auf verschiedenen Längengraden der Erde ein anderer ist, muss man bei der Ermittlung der Sternzeit also auch die geographische Länge des Beobachters berücksichtigen. Zur Einstellung eines Himmelsobjektes nach Koordinaten müssen wir also die Rektaszension wissen, und die Sternzeit. Die Sternzeit müssen wir aus der mittleren Sonnenzeit, das ist die Zeit die unsere Uhren anzeigen, und der geographischen Länge unseres Beobachtungsortes ermitteln.

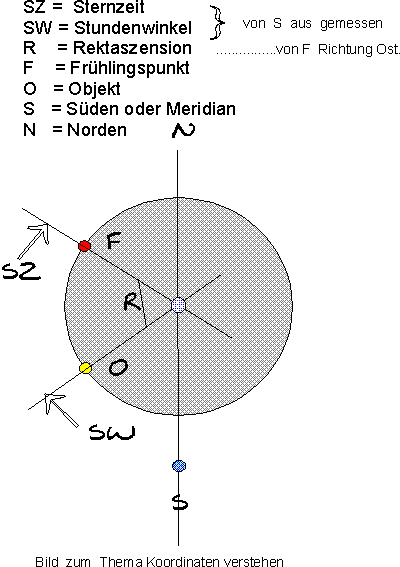
Der zur Einstellung eines Teleskops nötige Stundenwinkel kann also als Stundenwinkel = Sternzeit – Rektaszension berechnet werden. Der Stundenwinkel gibt den Winkel in Std. Min. und Sek. zum Meridian des Beobachtungsortes an.

Und nun sind wir fast am Ziel, was uns noch fehlt ist die Klärung einiger Begriffe wie „Zonenzeit“ und „Ortszeit„.

Die Zeit die unsere Uhren anzeigen beziehen sich auf den Lauf der Sonne. Der mittlere scheinbare Umlauf der Sonne um die Erde in Bezug auf den Meridian (Süden), also von Mittag zum Mittag des nächsten Tages wurde in 24 gleich große Zeitabschnitte eingeteilt, die Stunden. Da die Sonne 24 Stunden für diesen Umlauf benötigt ist an jedem Längengrad der Erde zu einem anderen Zeitpunkt Mittag.

Jeder Ort auf einem anderen Längengrad hat eine andere Zeit, eben die sogenannte „Ortszeit„. Wenn es im Null-Meridian 12 Uhr Mittags ist, so ist die Ortszeit in -9° z.B. 11h24m UT (Universal Time, das ist die Sonnenzeit des Null-Meridians) oder 12h24m MEZ (UT + 1 h ) da durch die Drehung der Erde von West nach Ost die Sonne in -9° früher im Mittag (Süden) stand. Man sieht also, die Ortszeit ändert sich mit dem Längengrad.

Und jetzt sehen wir auch warum unsere Uhren keine Ortszeit anzeigen, dies würde in Wirtschaft und Verkehr ein wahres Chaos anrichten. Auf der anderen Seite muss man sicherstellen, dass der Mittag, also der Höchststand der Sonne, schon so zwischen 12 Uhr und 13 Uhr stattfindet und nicht erst abends z. B. um 18 Uhr. Um dieses Problem zu lösen, hat man die „Zonenzeit“ eingeführt. Die bei uns übliche MEZ (Mitteleuropäische Zeit) ist die Ortszeit des 15. Längengrades Ost. Es gibt 12 Zonen zu je ca. 15° oder 1 Stunde Verschiebung. Die Einteilung wird freilich politischen Grenzen angepasst.

Ergänzend muss man noch die Sommerzeit MESZ erwähnen, die mit Astronomie überhaupt nichts zu tun hat, und eine willkürliche politische Festlegung ist, sie hat während einiger Monate im Jahr zur Sommerzeit Gültigkeit. Während dieser Zeit muss man von der Uhrzeit eine Stunde abziehen um auf MEZ zu kommen, das ist alles.

Um von der Zonenzeit auf die Ortszeit zu kommen, nehmen wir als Beispiel, MEZ auf 9° Ost, muss man 6° oder 24 min zur MEZ addieren. Nach Westen muss man immer die Zeitdifferenz addieren, nach OSTEN subtrahieren. Da – 9° westlich von – 15° (MEZ – Basis) liegt, muss die Zeitdifferenz addiert werden, wenn man MEZ als Bezugspunkt wählt. Nimmt man UT als Bezugspunkt muss man subtrahieren.

Nun haben wir alle Einzelheiten durchgekaut, und es wird höchste Zeit dass wir an einem praktischen Beispiel die letzten Unklarheiten beseitigen.

Einstellung des Teleskops auf ein Objekt am Himmel nach Koordinaten

Koordinaten des Himmelsobjektes (geozentrisch, d.h.auf den Mittelpunkt der Erde bezogen) z.B.

Rektaszension (R) = 17h 24,3m

Deklination (D) = -23°16′

Aus einem astronomischen Jahrbuch entnommen, waren dies die Daten von Uranus am 10. Mai 1986 um 1h30m MESZ.

Da sich die Deklination wie auf der Erde auf den Äquator bezieht können wir den abgelesenen Wert direkt am Teleskop einstellen. Das „-“ Zeichen sagt uns, dass das Objekt auf der südlichen Halbkugel ist, also 23°16′ südlich des Äquators.

Die Umrechnung der Rektaszension in Stundenwinkel:

• Sommerzeit kompensieren: MESZ – 1h = MEZ = 1h30m – 1h = 0h30m. Dann ist die mittlere Ortszeit z. B. auf 9° Ost: MEZ – 24m = 0h06m
• Sternzeitkorrektur (mittlere Ortszeit + Sternzeitkorrektur, zu entnehmen aus einem astronomischen Jahrbuch): 15h10m ergibt die Sternzeit 15h16m
• abzüglich der Rektaszension (R): 17h24,3m würde es einen negativen Wert ergeben, deshalb werden 12 Stunden addiert: +12h und es ergibt sich ein Stundenwinkel von 9h51,7m (wenn das Ergebnis größer 24 Std. wäre müsste man 24 Std. subtrahieren).

Wenn man das Teleskop nun auf den SW von 9h51,7m einstellt, und um 1h30m MESZ, die Nachführung des Teleskops einschaltet, ist das Objekt im Fernrohr zu sehen (falls man ein Objekt mit m = 8 erkennen kann).

Und nun wünsche ich viel Vergnügen bei einem Beispiel, das Sie sich selbst ausdenken und testen. Wenn das Objekt nicht sichtbar ist, liegt es weder am Teleskop noch an den Angaben im Sternkalender.

Willy Mahl 14.07.2000

---

Letzte Änderung am 2009-Mar-15