Geschichte der Entfernungsmessung in der Astronomie

Zu den ältesten und bis heute schwierigsten Fragen in der Astronomie gehört die Frage nach der Entfernung von Himmelsobjekten. Schon im Altertum hat die Suche nach Lösungen begonnen.

Ein berühmter, auch heute noch bekannter Versuch, die Entfernungen von Sonne und Mond zu ermitteln, wurde von Aristarch von Samos (ca. 300 v. Chr.) unternommen, indem er die zu dieser Zeit bereits bekannten Grund-Gesetze der Trigonometrie auf den Himmel übertrug und den Winkelabstand der Sonne vom Mond, in der Halbmondstellung des Mondes, gemessen hat:

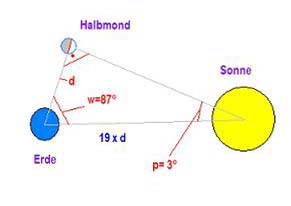
Sein Ergebnis war 87°. Daraus errechnete er dann das Verhältnis von Sonnen- und Monddistanz von der Erde, das bei diesen Winkelverhätnissen die Sonnendistanz = 19 fache Monddistanz ergab. Der wirkliche Wert weicht jedoch erheblich von dem Faktor 19 ab und liegt im Mittel bei 390. Um auf dieses Ergebnis zu kommen, hätte er einen Winkel von 89°59′ messen müssen. Ein Wert, der zum einen vermutlich seine Möglichkeiten bei weitem übertraf, und zum anderen zeigte, daß diese Messmethode äußerst problematisch ist, dabei ist an erster Stelle die Definition des Halbmondes zu nennen.

Ein weiterer origineller Versuch aus dem Altertum, die Mondentfernung von der Erde zu bestimmen wird auf Hipparch (160-125 v. Chr.) zurückgeführt. Er benutzte eine Mondfinsternis zur Lösung dieses Problems:

Er fand folgenden Zusammenhang für die Winkel:

ps + pm = p + s

Die Werte, die er zugrunde gelegt haben soll, waren für p = 15,5′;    s = 40,7′;    pm = 53,9′

pm ist die Mondparallaxe, die man auch durch die Messung der Zenitdistanzen des Mondes ermitteln kann.

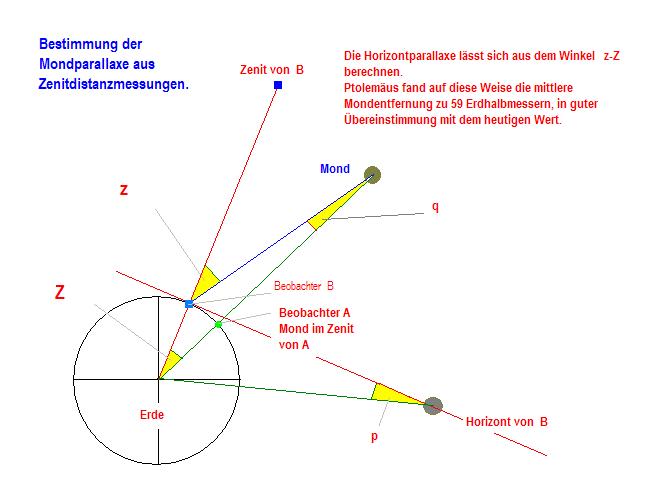
Aus: R_Erde / Rm = sin (pm) = sin 53,9′ = 0,0157 = 1 / 63,7 erhielt er dann den Mondbahnhalbmesser Rm = R_Erde * 63,7  =  405 833 km

Heute gelten folgende Werte: pm = 57′ (streut von 54′-61′ bei perigäischen und apogäischen Finsternissen) s = 41′; p = 15’44“ Anfang Juli und p = 16’16“ Anfang Januar.

Es hat dann aber mehr als 1500 Jahre gedauert, bis man genauere und bessere Lösungsansätze gefunden hat. Nachdem Kopernikus das heliozentrische Planetensystem postulierte und Kepler (1571-1630) im Gegensatz zu anderen führenden Astronomen seiner Zeit, von diesem System überzeugt war, hat er mit seinen nach ihm benannten drei Planeten-Gesetzen die Basis für die Vermeßung des Sonnensystems geschaffen.

Das 3. Keplersche Gesetz beschreibt den Zusammenhang von den Umlaufzeiten (T) zu den mittleren Bahnradien (R) der Planeten. In Worten ausgedrückt: Die Quadrate der Umlaufzeiten (T) sind proportional der 3. Potenz der Abstände ( R ). In eine Formel gebracht, lautet diese:

T² / R³ = const

Das gilt für jeden Planeten des Sonnensystems, wie auch für alle anderen Körper die eine zentrale Masse umkreisen. Auch für Monde, die einen Planeten umkreisen. Es ist const für Körper, die den gleichen Zentralkörper umlaufen gleich und so kann man schreiben:

T_Erde² / R_Erde³ = T_Mars² / R_Mars³ = T_Jupiter² / R_Jupiter³ = … usw.

Wenn man dann die Umlaufzeit in Jahren (Erde = 1), und die mittleren Bahnradien in Einheiten des Erde-Sonnenabstandes (=1) einsetzt, wird man die const = 1, und als Ergebnis für die Abstände der Planeten ein vielfaches der Erdentfernung bei den äußeren Planeten und einen Bruchteil davon bei den inneren Planeten.

Hierzu zwei Beispiele:

• T_Mars² / R_Mars³ = 1 , da die Umlaufzeit (T) von Mars 1,88 Jahre beträgt, erhält man für R = 1.52 fachen Erdabstand.
• T_Saturn² / R_Saturn³ = 1, T_Saturn ist knapp 30 Jahre, ergibt einen Wert für R_Saturn von knapp 10 fachen Erdabstand. Für Jupiter mit T = 12 Jahren , erhält man R = 5,2 usw.

Durch diesen Zusammenhang bekommt der Erdabstand von der Sonne eine besondere Bedeutung in der Vermessung des Sonnensystems .Man hat daher den mittleren Bahnradius der Erdbahn um die Sonne als 1 Astronomische Einheit = 1 AE definiert.

Damit bekam diese Entfernung eine zentrale Bedeutung, und musste möglichst genau vermessen werden. Die Ermittlung des Sonnenabstandes erwies sich jedoch als nicht einfach. Im Prinzip hätte man die Parallaxenmessung anwenden können, wenn 2 Beobachter mit möglichst großem Abstand auf der Erde (A,B) die Position der Sonne vor einem Hintergrund vermessen könnten.

Prinzip der Parallaxenmessung siehe Abb.

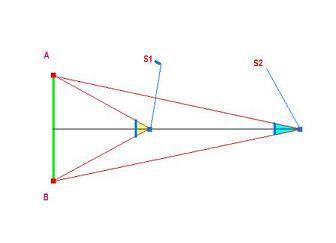
Ein Hintergrund wie z.B. die Fixsterne sind aber am Tag nicht sichtbar, aber selbst wenn ein Hintergrund vorhanden wäre , hätte man damit keinen Erfolg, denn der Abstand der Sonne (s) im Verhältnis zur möglichen Basis auf der Erde (A–B) ist viel zu gross um brauchbare Parallaxenwinkel zu erhalten.Es gibt jedoch am Himmel ein Ereignis, bei dem der Abstand des Messpunktes wesentlich näher ist als die Sonne , und bei dem auch der erforderliche Hintergrund, nämlich die Sonne, vorhanden ist.

Das Ereignis heißt Venus-Transit.

Es wurde nach der Idee von Edmond Halley (1656-1742) erstmals von ihm benutzt , um den Sonnenabstand von der Erde zu ermitteln. Aber auch hier ergaben sich einige Schwierigkeiten, obwohl das Prinzip auf den ersten Blick sehr elegant aussah. Es gab daher mehrere Lösungsansätze, die Halley’sche Methode siehe Abb.

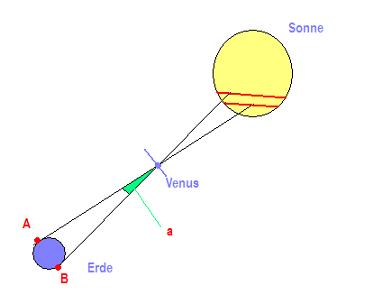
Die Beobachter in A und B registrieren die Dauer des Transits. Aus der Geschwindigkeit des Transits und dem scheinbaren Sonnenradius (ca.15′) ergibt sich die Länge der Sehnen, die parallel verlaufen.Daraus wurde der Parallaxenwinkel bestimmt. Diese einfache Methode war jedoch mit vielen Unsicherheiten meßtechnischer Art verbunden, und daher nicht genau. Durch zunehmende internationale Zusammenarbeit wurden jedoch die gemessenen Werte laufend verbessert, bis man sich dann beim Transit am 9.12.1874 auf einen Wert von 1 AE = 149 668 600 km einigte.

Es gab aber auch noch weitere Ideen die AE zu ermitteln. So hat man Ende August 1877 , als Mars eine günstige Perihelopposition hatte, auch diesen Anlass benutzt um mit der Marsparallaxe die AE zu ermitteln. Diese Methode führte zu dem Ergebnis 1 AE = 149 395 000 km.

In 1900 und 1941 wurde schließlich noch der Kleinplanet EROS benutzt, um die Messungen zu verbessern. Der punktförmige Eros war in größerer Erdnähe und bot dadurch weitere meßtechnische Vorteile gegenüber dem Mars und dem Venus- Scheibchen. Die ermittelten Werte entsprachen jedoch den Werten des Venustransits vom 9.12.1874.

In 1990 wurde der Venus Abstand mittels Radar Messung festgelegt. Seither gilt der Wert von 1 AE = 149 597 870 km.

Zusammenfassung der astronomischen Maßeinheiten :

1 AE (Astr.Einheit) = 1,496 * 10^8 km = 149,6 Mio km
1 LJ (Lichtjahr) = 9,46 * 10^12 km = 63 235 AE
1 pc (Parsec) = 3,26 LJ =  206 264,8 AE
1 kpc (kiloparsec ) = 1 000 pc
1 Mpc (Megaparsec) = 106 Pc

1 AE entspricht 8m20s Lichtlaufzeit und einer Sonnenparallaxe von p = 8,794„.

Unter der Sonnenparallaxe p versteht man den sehr kleinen Winkel unter dem von der Sonne aus gesehen der Erdradius (Äquatorhalbmesser) erscheint:

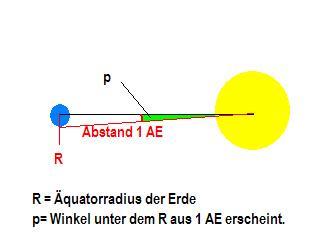
Die Elle des Astronomen ist die Parallaxenskunde, auch Parsec genannt (pc). Auch hier ist die AE die Basis, sie gibt die Entfernung an unter der 1 AE als 1 Bogensekunde erscheint. Die wesentlich größeren Entfernungen der Sterne von unserem Sonnensystem erlauben die Anwendung der Sternparallaxe jedoch nur bis zu einer Entfernung von ca. 100 pc, also um die 300 Lichtjahre, da ja die Basis der Messung, die Umlaufbahn der Erde, nicht vergrößert werden kann und damit die Winkel bei zunehmender Entfernung immer kleiner und damit zu ungenau werden.

Siehe Abb.

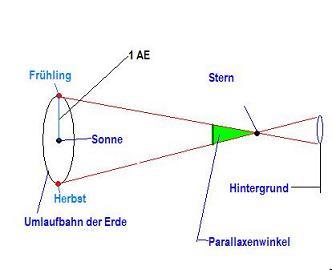
Die sonnennächsten Sterne sind:

Stern	Parallaxe	Entfernung	Absolute Helligkeit
Proxima Centauri	0,762″	1,31 Pc	15,1 mag
Alfa Centauri A, B	0,751″	1,33 Pc	4,4 mag / 5,8 mag
Barnards Pfeilstern	0,545″	1,83 Pc (Eigenbewegung 10,3″ / a=89 km/s) *
Wolf 359	0,427″	2,34 Pc	16,8 mag
Lalande	0,398″	2,51 Pc	10,5 mag
Sirius A, B	0,375″	2,67 Pc	1,4 mag / 11,5 mag

* In 100 Jahren bewegt er sich um ca. 1/2 Vollmondbreite (~15′)

Bis zu einer Entfernung von 12 Lichtjahren gibt es in der Sonnennachbarschaft 20 Sterne. Damit kommen wir zum nächsten Schritt hinaus in den Raum, der sogenannten

Sternstromparallaxe

Die Mitglieder eines Sternhaufens bewegen sich alle gemeinsam parallel im Raum. Bei einigen sogenannten offenen Haufen, die in unserer Nähe sind, kann man diese Bewegung beobachten. Durch den Perspektiven – Effekt bewegen sich die Sterne, ähnlich wie Eisenbahnschienen scheinbar auf einen gemeinsamen Fluchtpunkt zu, den sogenannten VERTEX. Damit ist die Richtung der räumlichen Bewegung bekannt. Die in Richtung des Beobachters gerichtete Raumkomponente, die sogenannte Radialgeschwindigkeit, kann man mit Hilfe des Dopplereffektes direkt in (km/s) ermitteln. Aus dieser Radialgeschwindigkeit und der bekannten Richtung der Raumgeschwindigkeit ergibt sich direkt die Geschwindigkeit der Komponente senkrecht zur Beobachtungsrichtung, also die Bewegung an der Himmelssphäre, ebenfalls in (km/s). Andererseits misst man diese Seitwärtsbewegung auch am Himmel im Winkelmaß, z.B. in Bogensekunden pro Jahr. Aus dem gemessenen Winkel und der Geschwindigkeitskomponente senkrecht zur Beobachtungsrichtung kann man die Entfernung ermitteln. Siehe folgende Abbildung, Sie zeigt die Koordinaten des offenen Haufens der Hyaden im Sternbild Stier.

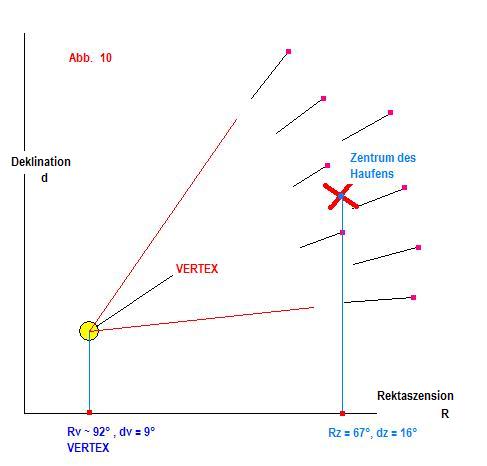
Die Methode der Entfernungsbestimmung zeigt folgende Prinzipskizze:

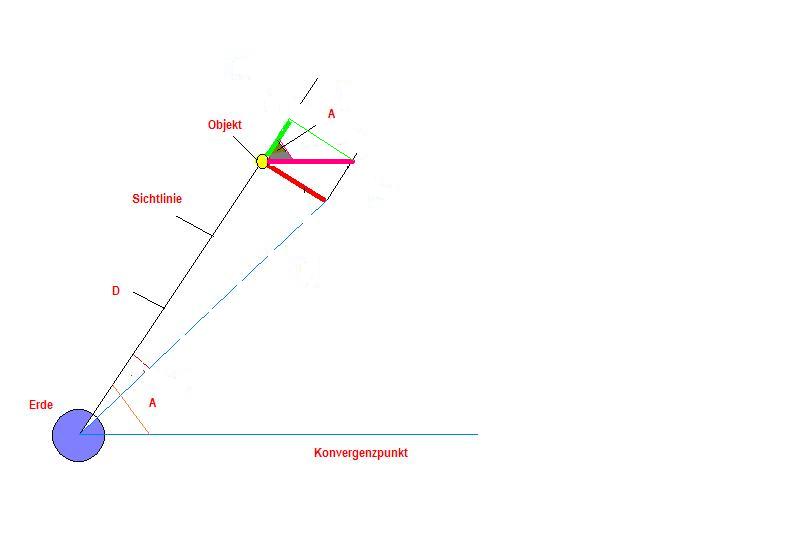
Die Hyaden beinhalten ca. 100 Sterne, die jedoch nicht alle dieselben physikalischen Eigenschaften haben. Daher haben sie auch verschiedene Leuchtkräfte bzw. absolute Helligkeiten M. Diese kann man nun über die geometrisch bestimmte Entfernung und ihre beobachtete Helligkeit ermitteln. Mit den 100 Sternen hat man eine beträchtliche Vielfalt von verschiedenen Sterntypen, deren Spektren man analysieren kann. Man teilt sie in Klassen ein nach der Struktur ihrer Linienspektren, und findet, dass Sterne der gleichen Spektralklassen auch annähernd dieselbe Leuchtkraft haben, wenn sie sich auf der Hauptreihe des Hertzsprung – Russel – Diagramms befinden. Die Entfernung der Hyaden wurde zu 46 pc ermittelt.

Die Grundeichung des astronomischen Entfernungssystems, ist die geometrisch bestimmte Entfernung der Hyaden.

Von den Hyaden weiter hinaus in den Raum wird als besonderer Meilenstein im Universum der Sterntyp der sogenannten Cepheiden-Veränderlichen benutzt. Man nennt sie Cepheiden weil sie zuerst im Sternbild Cepheus entdeckt wurden und Veränderliche weil sie periodischen Schwankungen der Helligkeit unterworfen sind.

Warum Cepheiden pulsieren

Ein Cepheiden-Veränderlicher ist ein vergleichsweise junger Stern mit der mehrfachen Masse der Sonne, dessen Helligkeit periodisch schwankt. Er wird dabei schnell heller, aber viel langsamer lichtschwächer. Ursache dieser Helligkeitsschwankug ist seine Pulsation. Diese radiale Schwingung kommt zustande, weil die Gaskugel nicht im hydrostatischen Gleichgewicht ist. Die Schwerkraft, die auf die Sternmaterie wirkt und diese zum Mittelpunkt zieht, wird nicht exakt vom Druck des heißen Gases und der Strahlung im Inneren, der die Materie nach außen zu treiben versucht, kompensiert. Das Ungleichgewicht beruht auf Veränderungen in der Sternatmosphäre. Ein wichtiger Bestandteil der Gashülle ist einfach ionisiertes Helium, da die Heliumatome infolge der hohen Temperatur eines ihrer beiden Elektronen verloren haben. Die aus dem Sternzentrum kommende Strahlung wird vom Helium absorbiert und gestreut, so dass auch noch das 2. Elektron vom Heliumkern abgespalten wird und somit das Heliumatom 2-fach ionisiert ist. Dadurch nimmt die „Opazität“ der Sternatmosphäre zu, das heißt die Strahlung aus dem Innern kann nicht mehr so gut passieren. Diese Wechselwirkung zwischen Strahlung und Materie, drückt die Atmosphäre nach außen. Der Stern wird größer und damit heller. Bei der Ausdehnung kühlt sich die Atmosphäre jedoch ab, so dass das 2x ionisierte Helium wieder 1 Elektron einfangen kann. Dadurch kann die Strahlung wieder besser nach außen dringen, der Druck auf die Atmosphäre nimmt dadurch wieder ab, so dass die Schwerkraft wieder überwiegt. Schließlich kollbiert die die Atmosphäre wieder auf Ihre ursprüngliche Größe. Der Stern erreicht seine ursprüngliche Helligkeit wieder und der Zyklus kann von Neuem beginnen. Mit Hilfe theoretischer Modelle zur Entwicklung des Sterninnern, und von Simulationen des Strahlungsflusses haben Astronomen das Schwingungsverhalten von Cepheiden mit hoher Genauigkeit nachvollziehen können. Da man die Physik der Cepheiden gut versteht und die jungen Sterne ausgiebig beobachtet hat, werden sie als sehr gute Entfernungsindikatoren eingestuft, man nennt sie daher auch „Standardkerzen“. Es gibt auch andere Arten von pulsierenden Sternen, hier eine Zusammenfassung.

Pulsierende Sterne eignen sich zur Entfernungsbestimmung und sind so zu Meilensteinen des Universums geworden. Es besteht eine feste Beziehung zwischen Periode und Helligkeit des Veränderlichen. Sterne mit längeren Perioden haben eine größere Leuchtkraft. RR-Lyrae Sterne sind kurzperiodische Veränderliche mit Perioden von unter einem Tag. Mira Sterne sind dagegen langperiodische Riesensterne mit Perioden bis zu 1000 Tagen. Die Cepheiden können mit dem bekannten Hyaden Sternhaufen geeicht werden. Gleiche Spektren haben gleiche Strahlungsleistung. Damit kann man aus den Hyaden deren Spektrum und Entfernung bekannt sind, die Entfernung eines Objektes über sein Spektrum ermitteln, wenn man die scheinbare Helligkeit kennt. Die Methode der Cepheiden-Veränderlichen kann bis zu einer Entfernung von ca. 10 Mio. LJ eingesetzt werden. Die Grenze ergibt sich aus der Beobachtbarkeit der Pulsation des Sterns.

Die Rotverschiebung

Eine weitere Möglichkeit, kosmische Entfernungen zu ermitteln, ist die sogenannte Rotverschiebung.

Genaue Messungen zeigen, dass man die Bewegung von Objekten nachweisen kann, indem man in ihrem Spektrum die Verschiebung eines Linienmusters eines bestimmten Elements beobachtet. Bewegt sich das Objekt auf den Beobachter zu, wird die Linie zum BLAUEN hin, bei der Fluchtbewegung zum ROTEN hin verschoben. Dies ist der Doppler-Effekt.1929 stellte Hubble fest, dass eine Relation zwischen Geschwindigkeiten und Entfernung von Galaxien besteht. Dies war der Ausgangspunkt für die Urknall Hypotese. Es zeigte sich, dass Rotverschiebung und Entfernung direkt proportional sind. Bei doppelter Entfernung haben die Galaxien auch eine doppelte Rotverschiebung. Diese einfache Beziehung nennt man das Hubble-Gesetz. Das ist das Gesetz das uns das expandierende Universum zeigt. Ob jedoch die Expansionsrate (Hubble Konstante) immer gleich groß war oder sein wird, weiss man nicht. Noch kann man nicht ausschliessen, dass die Expansion in eine Kontraktion übergeht. Selbst der Betrag der sogenannten Hubble Konstante ist derzeit noch umstritten.

Der Doppler-Effekt

Die Rotverschiebung hat ihre Ursache im Doppler-Effekt (DE). Mit dem DE kann man die radiale Geschwindigkeit in Blickrichtung eines Objekts im Weltraum bestimmen. Der DE bei elektromagnetischen Wellen, wie z.B. beim Licht,hat genau dieselben Ursachen wie wir sie im Schallbereich beobachten, und vor allem hören können. Die Änderung der Frequenz und damit der Tonhöhe einer näherkommenden, oder sich entfernenden Schallquelle ist eine beinahe tägliche Erfahrung. Beispiel ist eine pfeifende Lokomotive, oder einfach nur ein vorbeifahrendes Auto.

Zusammenfassung der geometrischen und photometrischen Parallaxenmessungen als gekoppelte Methoden zur Messung von Entfernungen im Universum.

Um tief in das Universum vorzudringen benötigt man naturgemäß mehrere Messmethoden da jede Methode ihre physikalischen Grenzen hat. Durch das 1 / r² Gesetz, dem auch eine elektromagnetische Strahlung wie das Licht gehorcht, müssen die Standardkerzen bzw. Bezugspunkte immer heller werden, je weiter man in den Raum vordringt. Denn nur aus dem beobachtbaren Licht können wir die notwendigen Informationen für die Entfernungsmessung erhalten.

Stufe 1

Ermittlung der Entfernung zum offenen Sternhaufen der Hyaden, über die geometrische Methode der Sternstromparallaxe. (auch kinematische Methode genannt). Reichweite ca. 150 Lichtjahre.

Stufe 2

Spektrumsvergleich von Hyaden Sternen mit anderen Sternen unserer Galaxie. Aus dem Spektrum der Hauptreihe des HR-Diagramms wird auf die Leuchtkraft geschlossen. Die geometrisch ermittelte Entfernung der Hyadensterne wird als Eichpunkt benutzt. Reichweite ca. 100 000 LJ, entsprechend der Dimensionn der Milchstrasse.

Stufe 3

Pulsierende Sterne, auch physikalische Veränderliche genannt, (nicht zu verwechseln mit Bedeckungsveränderlichen) wie z.B. delta Cephei-Veränderliche haben eine Reichweite bis zu ca. 4 Mpc. Die Entfernung des Andromedanebels wurde mit dieser Methode ermittelt. Seine Entfernung liegt bei 2,5 Mio LJ. Diese Methode reicht jedoch nicht bis um Virgo-Haufen, da man in dieser Entfernung keine Cepheiden mehr beobachten kann.

Stufe 4

In Galaxien leuchten gelegentlich Novae auf. So auch in den Galaxien des Virgo Haufens. Novae sind Standardkerzen mit großer Reichweite bis zu ca. 30 Mpc

Stufe 5

Für Entfernungen > 30 Mpc dienen SUPERNOVAE als Standardlichtquellen, die an den Galaxien der 4. Stufe geeicht werden. Diese Methode reicht bis ca. 100 Mpc.

Stufe 6

Bei der Vermessung von Galaxienhaufen wurden die hellsten elliptischen Galaxien alle in guter Näherung mit der gleiche Leuchtkraft gemessen. Nimmt man diese Objekte als Standardkerzen, so kann man diese Methode bis zu Entfernungen > 100 Mpc. anwenden. Wie man sehen kann, reihen sich also die Entfernungsbestimmungen hierarchisch hintereinander. Jede Methode liefert die Grundlage für die nächste. Am Anfang steht die Längenmessung einer Basisstrecke auf der Erde, der nächste Schritt zur Vermessung des Erdkörpers, und weiter zu den Entfernungen innerhalb unseres Sonnensystems (3. Keplersches Gesetz). Es folgen mit der Bahn der Erde um die Sonne als Basisstrecke (1 AE) die geometrischen Methoden (jährliche Parallaxe), die zu den umliegenden Fixsternen führen und die sog. Sternstromparallaxen zu bestimmten Sternhaufen. Daran schließen sich dann die photometrischen Methoden zu den entfernteren Objekten in unserer Galaxie, der Milchstrasse, an und mit sehr hellen Messobjekten sogar zu unseren Nachbargalaxien. Hier werden dann die Methoden für die größeren Entfernungen geeicht. Es ist offensichtlich, dass sich auch alle Fehler bzw. Ungenauigkeiten in dieser Hirarchie fortpflanzen, so dass die Entfernungen immer ungenauer werden je größer sie sind.

Willy Mahl , April 2004

---

Letzte Änderung am 2009-Mar-15